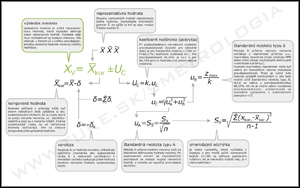
Základné pojmy Základné pojmy z metrológie vysvetlené čo najzrozumitelnejšie v grafickej, slovnej či matematickej podobe. Všetky pojmy sú vysvetlené teoreticky ale aj názorne na konkrétnych príkladoch zo života a strojárskej praxe. Výsledok merania Výsledok merania je definovaný reprezentatívnou hodnotou súboru korigovaných nameraných hodnôt a zohľadňuje celkovú neistotu merania. Tá sa udáva v štandardnom alebo rozšírenom tvare. Chyby a neistoty Chyba je definovaná ako rozdiel medzi nameranou a konvenčne správnou hodnotou. Neistota je parameter priradený k výsledku merania charakterizujúci rozptyl hodnôt, ktoré je možné racionálne priradiť k meranej veličine. Interval definovaný neistotou obsahuje skutočnú hodnotu veličiny. 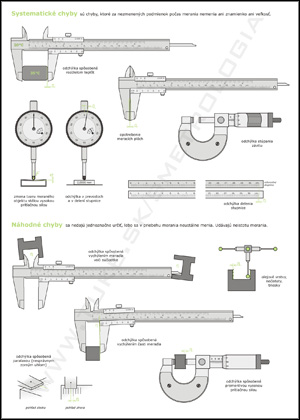Chyby sa delia na hrubé, systematické a náhodné. Hrubé chyby výrazne vybočujú z radu nameraných hodnôt. Ich hodnota je zjavne iná a je spôsobená napríklad nesprávnym zaobchádzaním s prístrojom prípadne. Systematické chyby sa v priebehu merania nemenia. Ich smer (znamienko) i veľkosť (hodnota) ostávajú konštantné a výsledok merania sa upravuje ich odčítaním. Korekcia je systematická chyba s opačným znamienkom. Náhodné chyby nie je možné jednoducho určiť. Počas merania sa menia a vplývajú na výsledok náhodne. Zdroje týchto chýb môžu byť rôzne... Neistoty delíme na typ A a typ B Neistoty typu A je možné zistiť štatisticky z radu nameraných hodnôt získaných za nezmenených podmienok Neistoty typu B sa získavajú z kalibračných certifikátov, technických údajov od výrobcu, skúseností z predošlých meraní, atď. 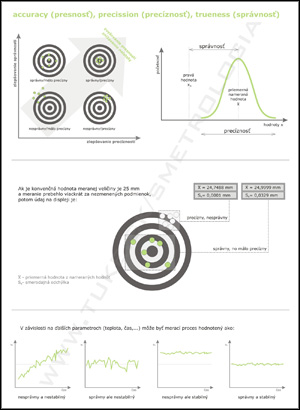Správnosť, presnosť, precíznosť Presnosť (z angl. accuracy) si možno predstaviť ako tesnosť zhody medzi nameranou hodnotou veličiny a pravou hodnotou veličiny. Pravá hodnota je z princípu v praxi neznáma. Precíznosť (z angl. precision) je tesnosť zhody medzi indikáciami alebo nameranými hodnotami veličiny získanými opakovanými meraniami na tom istom alebo podobných objektoch za špecifikovaných podmienok. Zvyčajne sa vyjadruje číselnými mierami nepresnosti ako napr. smerodajná odchýlka či rozptyl. Správnosť (z angl. trueness) je tesnosť zhody medzi priemerom nekonečného počtu opakovaných nameraných hodnôt veličiny a referenčnou hodnotou veličiny. Správnosť merania je nepriamo vztiahnutá iba k systematickej chybe merania. Nevzťahuje sa k náhodnej chybe merania. 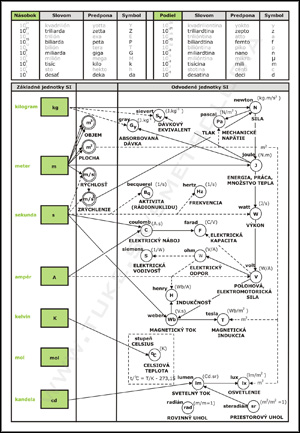Jednotky a veličiny Veličina je vlastnosť javu, telesa alebo látky, ktorá sa dá kvantitatívne rozlíšiť a kvantitatívne stanoviť. Veličiny toho istého druhu sa dajú zoskupovať do kategógií veličín. V rámci systému veličín sa odlišujú základné a odvodené veličiny. Medzi základné veličiny patria napríklad dĺžka, čas, hmotnosť, elektrický prúd, atď. Sú navzájom nezávislé. Rýchlosť je veličinou odvodenou. Tvoria ju veličiny základné - dĺžka a čas. Odvodené veličiny sa definujú pomocou matematických operácií. Jednotka je určitá reálna skalárna veličina, definovaná a prijatá dohodou, s ktorou sa porovnávajú ostatné veličiny toho istého druhu, aby sa vyjadrili ich veľkosti vzhľadom na túto veličinu. Meracie jednotky majú dohodou priradené názvy a symboly (značky). Hodnota veličiny je veľkosť určitej veličiny vyjadrená ako meracia jednotka vynásobená číslom. Číselná hodnota je podiel hodnoty veličiny a jednotky použitej na jeho vyjarenie. Napríklad hmotnosť balíka je m = 3,26 kg kde "m" je značka veličiny hmotnosť, "kg" je značka jednotky hmotnosti (kilogram) a "3,26" je číselná hodnota hmotnosti balíka vyjadrená v odpovedajúcej jednotke. Medzinárodný systém jednotiek (SI) je systém zavedený v roku 1960 jedenástou všeobecnou konferenciouo váhach a mierach. Sedem jednotiek: meter, kilogram, sekunda, ampér, kelvin, kandela a mól bolo prijatých za základné jednotky pre všetky medzinárodné váhy a miery. Sústava tolerancií a uložení Lícovanie je všeobecné označovanie presnosti obrábania a vzájomného vzťahu od seba závislých súčiastok, ktoré sú k sebe uložené alebo spolu spojené. Požadované lícovanie napr. pre uloženie hriadeľa v ložiskovom púzdre sa dosiahne voľbou tolerancií pre dieru a hriadeľ. Uloženie je vzájomný vzťah medzi rozmermi dvoch prvkov súčiastok (hriadeľa a diery), ktorý vyplýva z rozdielu ich rozmerov pred spojením. Obidva prvky pre spojenie majú spoločný menovitý rozmer. Vo vzájomnom vzťahu dvoch alebo viacerých plôch súčiastok môžu byť požadované nasledovné vlastnosti uloženia: - uloženie s vôľou (hybné) - umožňuje vzájomné otáčanie alebo posuv súčiastok, t.j. medzi hriadeľom a dierou je vždy vôľa, - uloženie prechodné - v tomto uložení sa môže vyskytnúť vôľa alebo presah; tolerancie diery a hriadeľa sa čiastočne prekrývajú, - uloženie s presahom (pevné) - zaručuje pri pôsobení predpokladaných funkčných síl a momentov nehybnosť spojenia, t.j. medzi hriadeľom a dierou je vždy presah. Veľkosť tolerancie a jej poloha voči nulovej čiare sú zakódované do tolerančnej značky (napr. H7 alebo k6). Písmeno udáva polohu tolerančného poľa a číslo udáva stupeň presnosti (veľkosť tolerancie). Tolerancia je tým väčšia, čím vúčšie je číslo označujúce stupeň presnosti a čím väčší je rozmer. Pre sústavu jednotného hriadeľa platí, že horný medzný rozmer je rovný menovitému rozmeru (uloženie h). Pre sústavu jednotnej diery platí, že dolný medzný rozmer je rovný menovitému rozmeru (uloženie H). Náhodné javy a pravdepodobnosť Niektoré deje sa chovajú tak, že pri zachovaní tých istých podmienok nikdy nie je isté, aký výsledok nastane. Určité výsledky nastanú častejšie než iné. Sú často závislé na činiteľoch, ktoré nedokážemé odhaliť. Preto sa im vraví deje náhodné a práve k nim sa viaže pojem pravdepodobnosť. Náhodné vplyvy pôsobia taktiež na meranie. Voľba rozdelenia pravdepodobnosti vychádza zo skúseností alebo teoretických znalostí o správaní sa náhodných dejov. Najčastejšie rozdelenia pravdepodobnosti sú: rovnomerné, normálne (Gaussovo), trojuholníkové (Simpsonovo), bimodálne trojuholníkové alebo bimodálne Diracovo. 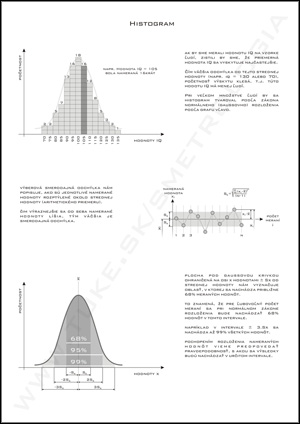Histogram je stĺpcový diagram, ktorého stĺce majú šírku veľkosti zvolených intervalov (v osi x) a výšku veľkosti príslušných absolútnych alebo relatívnych početností (v osi y). Normálne (tiež nazývané Gaussove) rozdelenie pravdepodobnosti je často sa vyskytujúce rozdelenie pravdepodobnosti spojitej náhodnej veličiny. Charakterizuje ho typický zvonovitý tvar. Gaussovo rozdelenie sa používa na aproximáciu v prípadoch, keď sa často vyskytuú malé odchýlky od menovitej hodnoty, pričom s rastúcou veľkosťou odchýlok pravdepodobnosť ich výskytu klesá. Rovnomerné (tiež nazývané pravouhlé) rozdelenie pravdepodobnosti sa používa v prípadoch, keď pravdepodobnosť výskytu malých odchýlok je v určitom intervale rovnaká ako pravdepodovnosť výskytu väčších odchýlok.